
A continuación se presenta un ejemplo de un sistema rotacional que presenta movimiento armónico simple cuando es desplazado de su posición de equilibrio. Por medio de un sistema de adquisición de datos se registra la posición angular del mismo a medida que está en movimiento. Al observar el resultado obtenido se encuentra que el sistema presenta un movimiento que además de ser armónico es amortigŁado.
El experimento corresponde a la versión rotacional del sistema masa - resorte. Está conformado por un disco con momento de inercia variable que se suspende por medio de un trozo de caucho de unos 7mm de diámetro. En la parte de abajo del disco se ubica el sensor de movimiento rotacional que registra la posición angular del disco a medida que se encuentra en movimiento.

En el experimento se estudia el comportamiento del sistema al variar el momento de inercia del disco. Inicialmente se disponen de manera simétrica las masas en el borde del disco y se realiza una medición de la posición angular del disco en función del tiempo. Posteriormente se acercan los discos al eje de rotación y se vuelve a realizar la medición.

En la siguiente figura se presenta el resultado obtenido para las configuraciones de las masas indicadas en verde y en rojo.
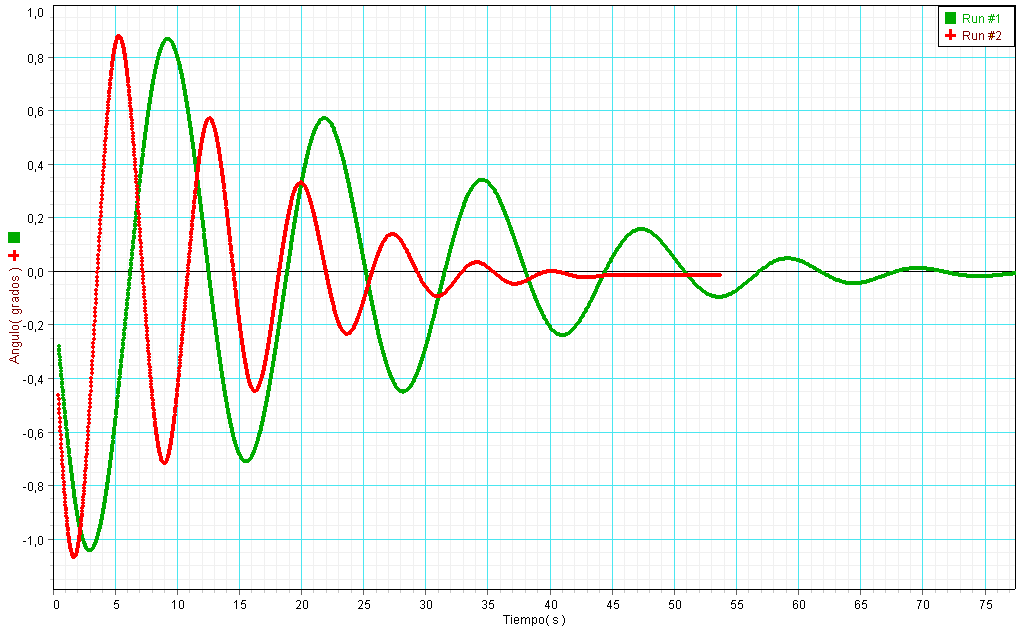
Del resultado es claro que la frecuencia con que oscila el sistema depende del momento de inercia del disco; en particular se encuentra que a medida que aumenta el momento de inercia (momento de inercia caso verde es mayor a momento de inercia caso rojo), la frecuencia de oscilación disminuye. Para obtener de manera teórica la frecuencia con que oscila el sistema, se considera que el pedazo de caucho se comporta como un análogo rotacional de un resorte ideal. Ahora la constante k relaciona un desplazamiento angular con un torque:
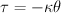
Suponiendo que el disco que se conecta al pedazo de caucho tiene momento de inercia I, se obtiene la ecuación diferencial que caracteriza el sistema:
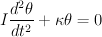
El coeficiente del segundo término corresponde al cuadrado de la frecuencia natural de oscilación. Se encuentra que esta depende de la constante k del pedazo de caucho y del momento de inercia del disco I, según la relación:
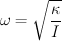
Que es consistente con el resultado experimental debido a que indica que a medida que aumenta el momento de inercia del disco, la frecuencia con que oscila el sistema disminuye.
Para iniciar la reproducción del video del experimento haga click en la imagen a continuación.