A continuación se presenta un montaje experimental que permite demostrar la aparición de ondas estacionarias circulares en un anillo de caucho que se hace vibrar. Considerando que el anillo representa la órbita seguida por el electrón alrededor del protón, y que el electrón puede visualizarse como una onda de materia, se encuentra que solo para ciertas frecuencias de vibración del sistema aparecen estados estacionarios. Estos corresponden, según la analogía establecida, a las órbitas estables planteadas por Bohr en su modelo.
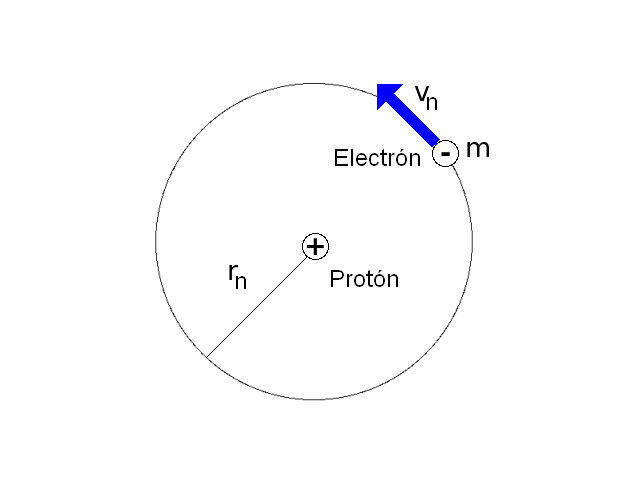
El modelo del átomo de hidrógeno planteado por Niels Bohr en 1.913 consiste en un núcleo conformado por un protón sobre el que gira un electrón siguiendo una órbita circular. El electrón no se precipita hacia el núcleo por acción de la fuerza electrostática existente entre las cargas debido a que hay ciertas órbitas estables en las que puede permanecer el electrón.

Cada órbita estable tiene asociado un radio y una energía que depende de un índice entero n. Estos estados estables surgen de la suposición de que el momento angular L del electrón está cuantizado según la relación:
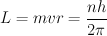
La suposición de que el momento angular está cuantizado no resulta del todo natural de interpretar; sin embargo si se combina esta hipótesis, con la relación propuesta por de Broglie, en donde el electrón tiene asociada una longitud de onda (λ = h / mv), se encuentra que las órbitas estables son aquellas en las que quedan inscritas exactamente un número entero de longitudes de onda; es decir son aquellas que satisfacen la siguiente condición:
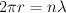
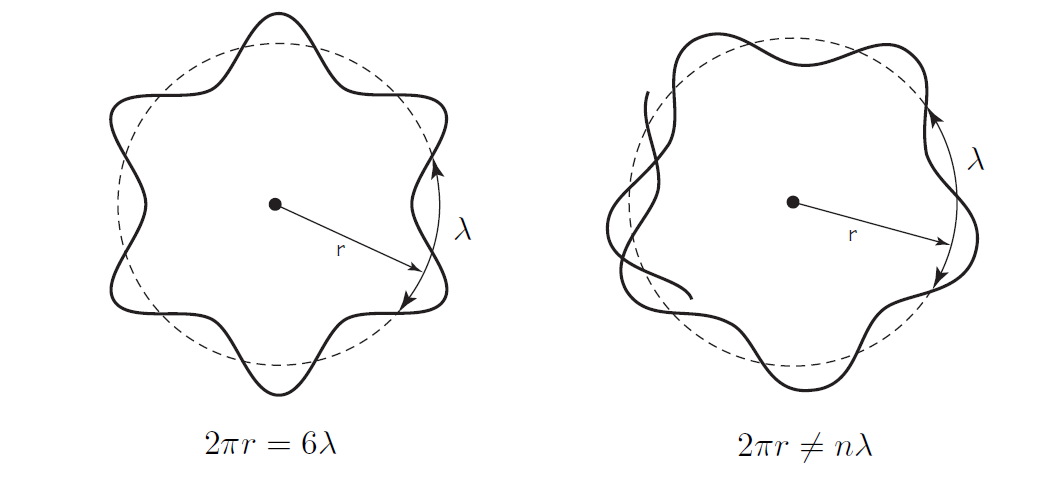
Se concluye entonces que las órbitas estables en donde permanece el electrón son aquellas en donde pueden quedar inscritas un número entero de longitudes de onda asociadas al electrón. En la siguiente figura se presentan dos casos de orbitas en donde una es permitida y la otra no.
El montaje experimental que se presenta a continuación permite recrear estados estacionarios en un anillo de caucho, que se asemejan bastante a los estados estacionarios asociados a las órbitas permitidas en el átomo de Bohr. El montaje está conformado por un anillo construido a partir de bandas de caucho. En uno de los extremos del anillo se conecta un eje metálico que sobresale del cono de un parlante. El eje oscila hacia arriba y hacia abajo con una frecuencia definida por el generador de señales conectado al parlante.

Cuando el sistema se pone en funcionamiento, el parlante hace que las bandas elásticas se muevan hacia arriba y hacia abajo. Al aumentar gradualmente la frecuencia, se encuentra que hay ciertos estados particulares en donde el movimiento de las bandas elásticas es bien definido debido a que aparecen nodos y antinodos que permanecen estáticos en el anillo.

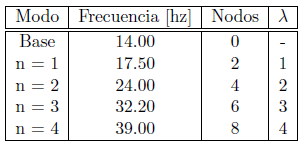
El primer modo estacionario aparece a una frecuencia de 14Hz. En este estado el anillo se mueve al unísono hacia arriba y hacia abajo; no hay nodos ni antinodos, sin embargo el comportamiento de la oscilación es bien definido. A medida que se aumenta la frecuencia, aparece el primer modo excitado (n=1), en donde se observan dos nodos opuestos, que corresponden a una longitud de onda completa inscrita en el anillo de caucho. El segundo modo excitado (n=2) aparece a una frecuencia de 24.0Hz. En este modo, se observan cuatro nodos, que corresponden a dos longitudes de onda completas inscritas en el anillo. En la siguiente tabla se presenta un resumen de todos los estados estacionarios observados en el montaje experimental.
En el modelo mecánico el anillo representa la órbita seguida por el electrón alrededor del protón y el electrón, dada su naturaleza ondulatoria, se modela como el conjunto de ondas que viajan a lo largo del anillo de caucho. En el experimento se observa que en solo ciertas frecuencias específicas aparecen estados estacionarios, que satisfacen la relación \ref{eq:AtomoBohr-CondicionOrbitaBroglie} y que dada la analogía establecida, corresponden a las órbitas permitidas en donde puede estar el electrón.
En la siguiente figura se presentan imágenes correspondientes a los tres primeros modos excitados del sistema. En cada imagen se señala la posición de los nodos. Para el modo n=1 (17.5 Hz - 2 nodos) aparece una longitud de onda completa a lo largo de la circunferencia de la "orbita". En el modo n=2 (24.0 Hz - 4 nodos), aparecen dos longitudes de onda completas y en el tercer modo excitado n=3 (32.2 Hz - 6 nodos), aparecen tres longitudes de onda completas. Se observa que el número de longitudes de onda completas en la circunferencia aumenta en uno cada vez que el índice n aumenta en una unidad.

Rubber band Bohr wave functions - The Physics Teacher - Phys. Teach. 47 310 (2009)