En el experimento en donde se hacen colisionar la pelota de tenis con la de baloncesto (consultar experimento colisión entre pelotas con diferente masa) se observa que la altura final de la pelota de tenis es menor a nueve veces la altura inicial, como plantea el desarrollo teórico del experimento. Esto ocurre debido a que en el desarrollo teórico se asume que la colisión entre las pelotas es elástica. En la práctica esto no ocurre porque parte de la energía (potencial) inicial disponible se pierde en las colisión de la pelota de baloncesto con el piso y en la colisión entre las pelotas. En el siguiente experimento se presenta una forma de caracterizar esta pérdida de energía por medio de una cantidad llamada "coeficiente de restitución".
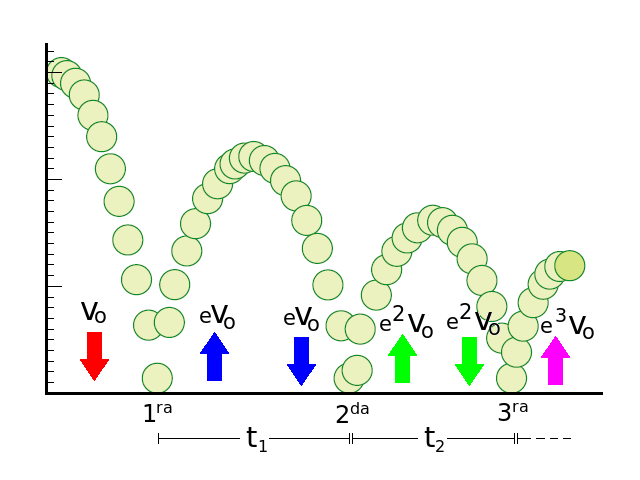
En el experimento se suelta una pelota de tenis desde una altura conocida. Se observa que a medida que rebota con el piso, va perdiendo altura hasta que se detiene. La pelota pierde altura cada vez que rebota debido a que la velocidad después de la colisión con el piso es e veces la velocidad antes de la colisión (e < 1). La cantidad e es conocida como el "coeficiente de restitución".
Una forma de calcular el parámetro e para la pelota de tenis de manera indirecta (el cálculo es válido para el caso en donde el coeficiente de restitución es constante en el tiempo) es a partir del tiempo que tarda la pelota en quedar en reposo después de que ha sido lanzada desde una altura conocida. Como se muestra a continuación, el tiempo es función del coeficiente e y de la velocidad inicial v0 antes de que la pelota rebote por primera vez.

El tiempo total que tarda la pelota en quedar en reposo corresponde a la suma de los tiempos entre rebotes sucesivos. En la figura se muestran los tiempos para las dos primeras colisiones denominadas t1 y t2 respectivamente. En general, el tiempo asociado al i-ésimo rebote es:
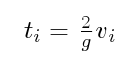
en donde vi corresponde a la velocidad de la pelota al inicio del i-ésimo rebote. Teniendo en cuenta la definición del coeficiente de restitución se pueden determinar los tiempos correspondientes a un número n de rebotes:
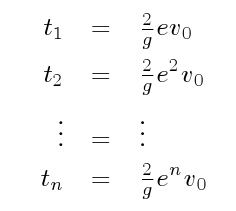
Para determinar el tiempo total T que tarda la pelota en quedar en reposo, se suman infinitos intervalos de tiempo:
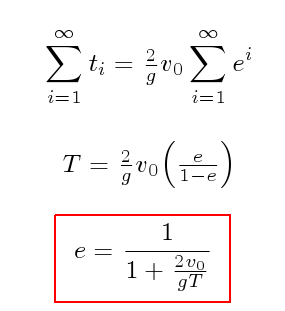
En donde es claro que entre más tiempo tarde la pelota en llegar al reposo, el coeficiente e será mas cercano a la unidad.
Para iniciar la reproducción del video del experimento haga click en la imagen a continuación.
Debouncing a superball - The physics teacher PDF